08 우선순위 큐 Priority Queue

출처

C언어로 쉽게 풀어쓴 자료구조(천인국, 공용해, 하상호 저)

1. 우선순위 큐의 개념

1-1. 우선순위 큐란?

우선순위 큐(Priority Queue)는 우선순위를 가진 항목들을 저장하는 큐로 FIFO(First In First Out) 순서가 이닌 순위가 높은 데이터가 먼저나가는 자료구조를 말한다.

스택 큐, 우선순위 큐 비교

자료구조	우선 삭제되는 요소
스택	가장 최근에 들어온 데이터
큐	가장 먼저 들어온 데이터
우선순위 큐	가장 우선순위가 높은 데이터

우선순위 큐는 시뮬레이션 시스템, 네트워크의 트래픽 제어, 운영체제 작업스케줄링 등에 사용된다.

1-2. 우선순위 큐의 기능

우선 순위 큐의 추상 자료형(ADT)를 살펴보자.

·객체: n개의 element형의 우선 순위를 가진 요소들의 모임

·연산: 
▪ create() ::= 우선순위큐를 생성한다.
▪ init(q) ::= 우선순위큐 q를 초기화한다.
▪ is_empty(q) ::= 우선순위큐 q가 비어있는지를 검사한다. 
▪ is_full(q) ::= 우선순위큐 q가 가득 찼는가를 검사한다.
▪ insert(q, x) ::= 우선순위큐 q에 요소 x를 추가한다.
▪ delete(q) ::= 우선순위큐로부터 가장 우선순위가 높은 요소를 삭제하고 이 요소를 반환한다.
▪ find(q) ::= 우선순위가 가장 높은 요소를 반환한다.

위 기능 중에서 가장 중요한 연산은 insert(삽입) 연산과 delete(삭제) 연산이다. 삽입, 삭제의 우선순위를 어떻게 정하느냐에 따라 최소 우선순위 큐와 최대 우선순위 큐로 분류를 나눌 수 있다.

1-3. 우선순위 큐의 표현방법

우선순위 큐를 구현하는 방법은 아래와 같다.

배열을 이용한 우선순위 큐
연결리스트를 이용한 우선순위 큐
히프(heap)를 이용한 우선수위 큐

시간복잡도 비교

표현방법	삽 입	삭 제
순서없는 배열	O(1)	O(n)
순서없는 연결 리스트	O(1)	O(n)
정렬된 배열	O(n)	O(1)
정렬된 연결 리스트	O(n)	O(1)
히프	O($log_2{n}$)	O($log_2{n}$)

시간 복잡도에서 히프가 유리하다는 것을 알 수 있다.

2. 히프

2-1. 히프란?

히프(heap)는 뭔가가 쌓여있는 '더미' 모습과 비슷하며 붙여진 이름으로, 완전이진트리를 기반으로 하고 있다. 기본적으로 노드의 키들은 아래의 식을 만족한다.(최대 히프)

$$ 부모노드의; key\quad\geqq\quad 자식노드의 key; $$

또한 히프트리는 중복된 값을 허용할 수 있다. 히프는 우선순위 큐와 마찬가지로 우선순위의 기준에 따라 종류가 나뉜다.

최대 히프(max heap): $ 부모노드의; key\quad\geqq\quad 자식노드의 key; $
최소 히프(min heap): $ 부모노드의; key\quad\geqq\quad 자식노드의 key; $

n 개의 노드를 가지고 있는 히프의 높이 h는 $log_2{n}$ 과 같다

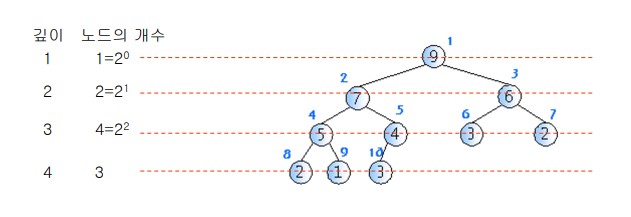
cf) 주의사항!! 자료구조 Heap과 메모리 영역인 Heap은 완전히 다른 개념이다!!

2-2. 배열을 이용한 구현

히프는 완전이진트리이므로 각 노드에 번호를 붙일 수 있다. 이 번호를 배열의 인덱스라고 생각하고 구현을 하면 된다.

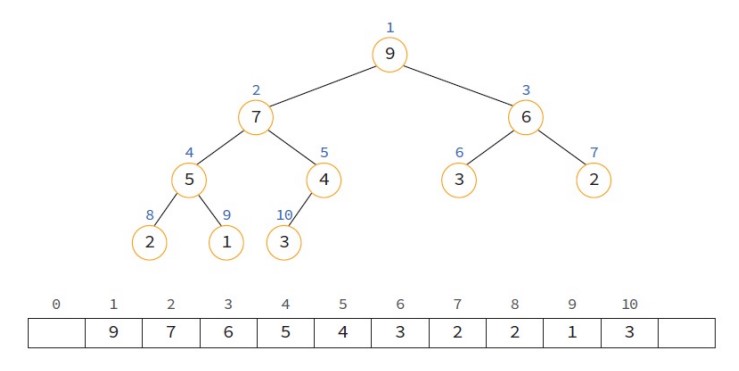
배열로 히프를 구현하면, 부모노드와 자식노드를 찾는 것이 굉장히 쉽다. 이 방식은 아래와 같은 원리를 따른다.

왼쪽 자식의 인덱스 = (부모의 인덱스)*2
오른쪽 자식의 인덱스 = (부모의 인덱스)*2 + 1
부모의 인덱스 = (자식의 인덱스)/2

히프는 아래와 같이 정의할 수 있다.

#define MAX_ELEMENT 200

typedef struct {
   int key;
} element;

typedef struct {
   element heap[MAX_ELEMENT];
   int heap_size;
} HeapType;

HeapType heap;             // 정적 메모리 할당 사용
HeapType *heap = create(); // 동적 메모리 할당 사용

히프에서 가장 중요한 연산은 삽입연산과 삭제연산이다. 자세한 설명은 아래와 같다.

삽입 연산(upheap)
1. 히프에 새로운 요소가 들어 오면, 일단 새로운 노드를 히프의 마지막 노드에 이어서 삽입
2. 삽입 후에 새로운 노드를 부모 노드들과 교환해서 히프의 성질을 만족

삭제 연산(downheap)
1. 루트 노드를 삭제
2. 마지막 노드를 루트 노드로 이동
3. 루트에서부터 단말 노드까지의 경로에 있는 노드들을 교환하여 히프 성질을 만족

히프 코드: 링크

3. 우선순위 큐 응용

3-1. 히프 정렬

히프를 이용해 정렬을 하는 방법이다. 정렬할 요소들을 최대힙에 삽입한 다음, 한 번에 하나씩 요소를 히프에서 삭제해서 배열에 저장하면 내림차순으로 저장할 수 있다. 여기서 거꾸로 뒤집으면 오름차순으로 표현할 수 있다. 일반적으로 최소힙을 사용하면 오름차순으로 정렬할 수 있다.

삽입하거나, 삭제할 때 시간 복잡도가 O($\log{n}$)만큼 소요되고 요소의 개수가 n개이므로 전체적인 시간 복잡도는 O($n\log{n}$)이다. 히프 정렬이 유용히 쓰이는 경우는 가장 큰 값 혹은 작은 값 몇개만 필요할 때이다. (ex- top 10 등)

히프 정렬 코드: 링크

3-2. 머신 스케줄링

만약 어떤 작업을 처리하는 기계가 m개 존재하고 처리할 작업이 n개 존재하면 이 m개의 기계들로 최소의 시간안에 작업들을 모두 끝내는 것이 가장 효율적일 것이다. 이 문제에 대해 최적의 해를 구하는 것은 매우 어렵지만 근사 해는 우선순위 큐를 활용하여 쉽게 찾을 수 있다.

아래 코드는 여러 스케줄링 기법 중 가장 긴 작업을 우선적으로 기계에 할당하는 LPT(Longest Processing Time first)방식이다. 기계가 꽉 찼을 때는 Job을 할당하지 않다가 비는대로 남은 Job 중 제일 긴 것을 할당한다.

머신 스케줄링 코드: 링크

3-3. 허프만 코드

아래와 같은 빈도수를 가진 문자 5개를 3개의 고정 비트(총 8개의 문자 표현 가능)를 이용해 고유값을 각각 할당하면 아래와 같을 것이다.

글자	비트 코드	빈도수	총 비트 수
e	000	15	3 * 15 = 45
t	001	12	3 * 12 = 36
n	010	8	3 * 8 = 24
i	011	6	3 * 6 = 18
s	100	4	3 * 4 = 12
합계			135

총 135비트가 쓰인다. 위의 경우는 글자수가 별로 없지만 만약 글자 수가 엄청나게 많다면, 압축의 과정은 필수적일 것이다. 이 때 사용하는 것이 허프만 코드이다. 허프만 코드의 알고리즘은 메시지의 모든 글자를 카운트해 빈도수를 구하고, 빈도수에 따라 트리를 만든다. 최소힙을 이용해 빈도가 가장 적은 트리 2개씩 묶어 하나의 트리가 될 때가지 합친다. 그 과정은 아래의 그림과 같다.

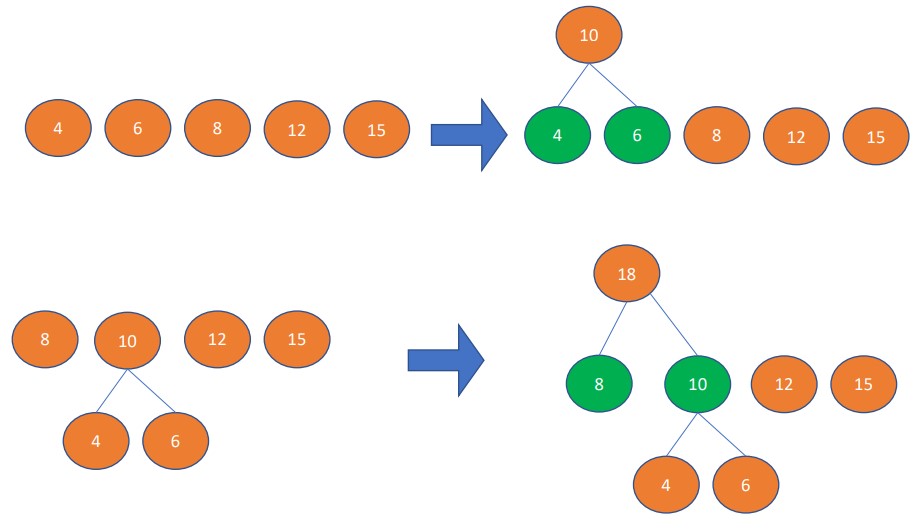
트리가 완성되면 각 글자에 대한 코드를 비트로 만들 수 있다. 해당 글자로 가는 경로를 센다. 위 그림은 왼쪽에 가중치를 1을 두고, 오른쪽에 0을 뒀지만, 둘을 바꿔 반대로 할 수도 있다. 위 트리를 통해 만든 비트체계는 아래와 같다.

글자	트리로 만든 비트 코드	빈도수	총 비트 수
e	00	15	30
t	01	12	24
n	11	8	16
i	100	6	18
s	101	4	12
합계			88

135 - 85 = 50(비트)를 아낄 수 있다. 위의 경우, 약 37%의 용량을 아낄 수 있었다.

허프만 코드: 링크

[자료구조] 우선순위 큐 Priority Queue

08 우선순위 큐 Priority Queue

출처

목차

1. 우선순위 큐의 개념

1-1. 우선순위 큐란?

1-2. 우선순위 큐의 기능

1-3. 우선순위 큐의 표현방법

2. 히프

2-1. 히프란?

2-2. 배열을 이용한 구현

3. 우선순위 큐 응용

3-1. 히프 정렬

3-2. 머신 스케줄링

3-3. 허프만 코드

티스토리툴바